График Функции Косинуса Презентация
Чтобы посмотреть презентацию с картинками, оформлением и слайдами, скачайте ее файл и откройте в PowerPoint на своем компьютере. Текстовое содержимое слайдов презентации: Тригонометрические функции, их свойства и графики В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто геометрический характер и представляла главным образом «исчисление хорд».
График Синуса
- Вы можете изучить и скачать доклад-презентацию на тему Презентация на тему Графики функций синуса и косинуса и их свойства. Презентация на заданную тему содержит 19 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки! Презентации» Алгебра» Презентация Презентация на тему Графики функций синуса и косинуса и их свойства. Слайды и текст этой презентации. Описание слайда: Графики и свойства тригонометрических функций синуса и косинуса.
- В качестве примера воспользуемся презентацией «Функция y = cos x. Её свойства и график». Эта презентация была создана для изучения и закрепления одной из тем в разделе «Тригонометрия». Большие трудности при изучении темы «Тригонометрические функции» возникают из-за несоответствия между достаточно большим объемом содержания и небольшим количеством часов, выделенным на изучение данной темы. Одним из решением данной проблемы может быть использование ИКТ на уроках математики. Презентация «Функция y = cos x. Её свойства и график» предназначена. Для изучения нового материала; предъявления новой инфо.
- Графики и свойства тригонометрических функций синуса и косинуса. - презентация. Презентация была опубликована год назад пользователемТатьяна.
Со временем в нее начали вкрапляться некоторые аналитические моменты. В первой половине 18-го века произошел резкий перелом, после чего тригонометрия приняла новое направление и сместилась в сторону математического анализа. Именно в это время тригонометрические зависимости стали рассматриваться как функции. В настоящее время изучению тригонометрических функций именно как функций числового аргумента уделяется большое внимание в школьном курсе алгебры и начал анализа. Существует несколько различных подходов к преподаванию данной темы в школьном курсе, и учитель, особенно начинающий, легко может запутаться в том, какой подход является наиболее подходящим.
Текстовое содержимое слайдов презентации: Тригонометрические функции, их свойства и графики В древности тригонометрия возникла в связи с потребностями астрономии, землемерия и строительного дела, то есть носила чисто геометрический характер и представляла главным образом «исчисление хорд». Со временем в нее начали вкрапляться некоторые аналитические моменты. В первой половине 18-го века произошел резкий перелом, после чего тригонометрия приняла новое направление и сместилась в сторону математического анализа.. Называется отношение косинуса угла х к синусу угла х. Обратныетригонометрические функции. Для sin х, cos х, tg х и ctg х можно определить обратные функции.
А ведь тригонометрические функции представляют собой наиболее удобное и наглядное средство для изучения всех свойств функций (до применения производной), а в особенности такого свойства многих природных процессов как периодичность. Поэтому их изучению следует уделить пристальное внимание. Кроме того, большие трудности при изучении темы «Тригонометрические функции» в школьном курсе возникают из-за несоответствия между достаточно большим объемом содержания и относительно небольшим количеством часов, выделенным на изучение данной темы. Таким образом, проблема этой исследовательской работы состоит в необходимости устранения этого несоответствия за счет тщательного отбора содержания и разработки эффективных методов изложения данного материала.
Объектом исследования является процесс изучения функциональной линии в курсе старшей школы. Предмет исследования - методика изучения тригонометрических функций в курсе алгебры и начала анализа в 10-11 классе.
Таким образом, основной целью создания данной работы является изучение темы: «Тригонометрические функции» в курсе алгебры и математического анализа. Тригонометрические функции — математические функции от угла. Они важны при изучении геометрии, а также при исследовании периодических процессов. Обычно тригонометрические функции определяют как отношения сторон прямоугольного треугольника или длины определённых отрезков в единичной окружности. Более современные определения выражают тригонометрические функции через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на произвольные вещественные числа и даже на комплексные числа. В изучении тригонометрических функций можно выделить следующие этапы:I. Первое знакомство с тригонометрическими функциями углового аргумента в геометрии.
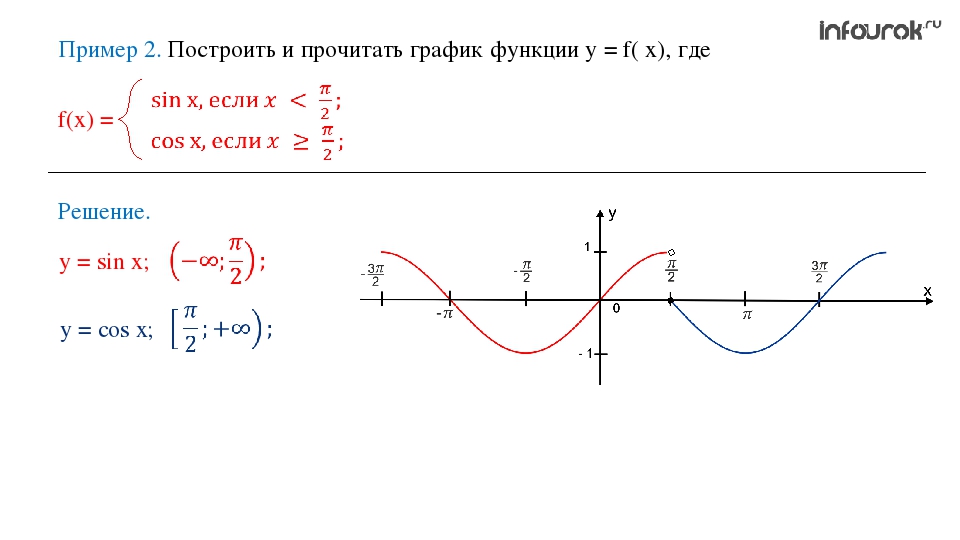
Значение аргумента рассматривается в промежутке (0о;90о). На этом этапе учащиеся узнают, что sin, сos, tg и ctg угла зависят от его градусной меры, знакомятся с табличными значениями, основным тригонометрическим тождеством и некоторыми формулами приведения.II. Обобщение понятий синуса, косинуса, тангенса и котангенса для углов (0о;180о).
На этом этапе рассматривается взаимосвязь тригонометрических функций и координат точки на плоскости, доказываются теоремы синусов и косинусов, рассматривается вопрос решения треугольников с помощью тригонометрических соотношений.III. Введение понятий тригонометрических функций числового аргумента.IV. Систематизация и расширение знаний о тригонометрических функциях числа, рассмотрение графиков функций, проведение исследования, в том числе и с помощью производной. Существует несколько способов определения тригонометрических функций. Их можно подразделить на две группы: аналитические и геометрические. К аналитическим способам относят определение функции у = sin х как решения дифференциального уравнения f (х)=-c.f(х) или как сумму степенного ряда sin х = х - х3 /3!+ х5 /5! К геометрическим способам относят определение тригонометрических функций на основе проекций и координат радиус-вектора, определение через соотношения сторон прямоугольного треугольника и определения с помощью числовой окружности.
В школьном курсе предпочтение отдается геометрическим способам в силу их простоты и наглядности. Определение синуса Синусом угла х называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол х (обозначается sin x). Определение косинуса Косинусом угла х называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол х (обозначается cos x). Определение тангенса Тангенсом угла х называется отношение синуса угла х к косинусу угла х. Определение котангенса Котангенсом угла х называется отношение косинуса угла х к синусу угла х. Обратныетригонометрические функции. Для sin х, cos х, tg х и ctg х можно определить обратные функции.
Они обозначаются соответственно arcsin х (читается «арксинус x»), arcos x, arctg x и arcctg x. А это основные тригонометрические формулы,которыми пользуются учащиеся во время решения тригонометрических задач. Тригонометрия- это наука, о которой можно говорить, рассказывать и писать БЕСКОНЕЧНО! Это одна из составляющих наук на многих факультетах институтов нашей страны!!!Это одна из тех наук, в которую были вложены труды таких ученых, как Евклид, Архимед, Аполлоний, Птолемей, Ф.Виет, И.Бернулли, Н.И.Лобачевский, Д.Е.Меньшов, Н.К.Бари и многих, многих других!!!
И в заключении хотелось бы сказать,.
Косинус Синус
Таблица Синусов И Кос
Напоминаем, что в соответствии с профстандартом педагога (утверждён Приказом Минтруда России), если у Вас нет соответствующего преподаваемому предмету образования, то Вам необходимо пройти профессиональную переподготовку по профилю педагогической деятельности. Сделать это Вы можете дистанционно на сайте проекта 'Инфоурок' и получить диплом с присвоением квалификации уже через 2 месяца! Только сейчас действует СКИДКА 50% для всех педагогов на все 111 курсов профессиональной переподготовки!
Доступна рассрочка с первым взносом всего 10%, при этом цена курса не увеличивается из-за использования рассрочки! Описание слайда: Свойство 1. D(y) = (-∞;+∞). Y = sin x – нечетная функция. Функция y = sin x убывает на отрезке -π/2+2πk; π/2 + 2πk и возрастает на отрезке π/2 + 2πk; 3π/2 + 2πk , где k є Z. Функция ограничена и сверху и снизу (-1 ≤ sin t ≤ 1).
Yнаим = -1; yнаиб = 1. Функция y = sin x периодическая, ее основной период равен 2π. Y = sin x – непрерывная функция. E(y) = -1;1.
Функция выпукла вверх на отрезке 0 + 2πk; π + 2πk, выпукла вниз на отрезке π + 2πk; 2π + 2πk, где k є Z. Описание слайда: Свойство 1. D(y) = (-∞;+∞). Y = cos x – четная функция. Функция y = cos x убывает на отрезке 2πk; π + 2πk и возрастает на отрезке π + 2πk; 2π + 2πk , где k є Z.
Функция ограничена и сверху и снизу (-1 ≤ cos t ≤ 1). Yнаим = -1; yнаиб = 1. Функция y = cos x периодическая, ее основной период равен 2π. Y = cos x – непрерывная функция. E(y) = -1; 1. Функция выпукла вверх на отрезке -0,5π+2πk; 0,5π+2πk, выпукла вниз на отрезке 0,5π+2πk; 1,5π+2πk, где k є Z. ' Описание материала: Данная презентация выполнена по теме «Тригонометрические функции, их свойства и графики».
Работа выполнена ученицей десятого класса. Цель - изучить сходства и различия в графиках и свойствах тригонометрических функций. Задачи презентации: дать определения тригонометрическим функциям, рассмотреть графики и свойства функций, сравнить полученные результаты. Презентация позволяет наглядно продемонстрировать данную тему, научить детей сравнивать, находить сходства и различия, развивает интерес у учащихся к выбранной теме. Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!
График Котангенса
Мнение редакции может не совпадать с точкой зрения авторов. Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.